Research Areas
This page presents some examples of our current research projects. If you are interested in one of the topics please contact us by email for further detailed information and check out our publications page where you can find papers, software, and additional download material.

The simulation of incompressible fluids like water is an important and active research topic in computer graphics. An application area is the generation of special effects where a main goal is the realistic simulation of incompressible fluids in turbulent scenarios. In the field of fluid dynamics we investigate simulation methods based on Smoothed Particle Hydrodynamics (SPH) which is a meshless Lagrangian approach to simulate complex fluid effects. In this research area we develop new methods for the efficient and stable simulation of incompressible fluids, highly viscous fluids and turbulent flow. Moreover, we publish our research in our open-source framework SPlisHSPlasH (see below).
See also our papers:
and our open-source framework:Supported by the German Research Foundation (DFG) as part of the Sonderforschungsbereich (SFB) 1120
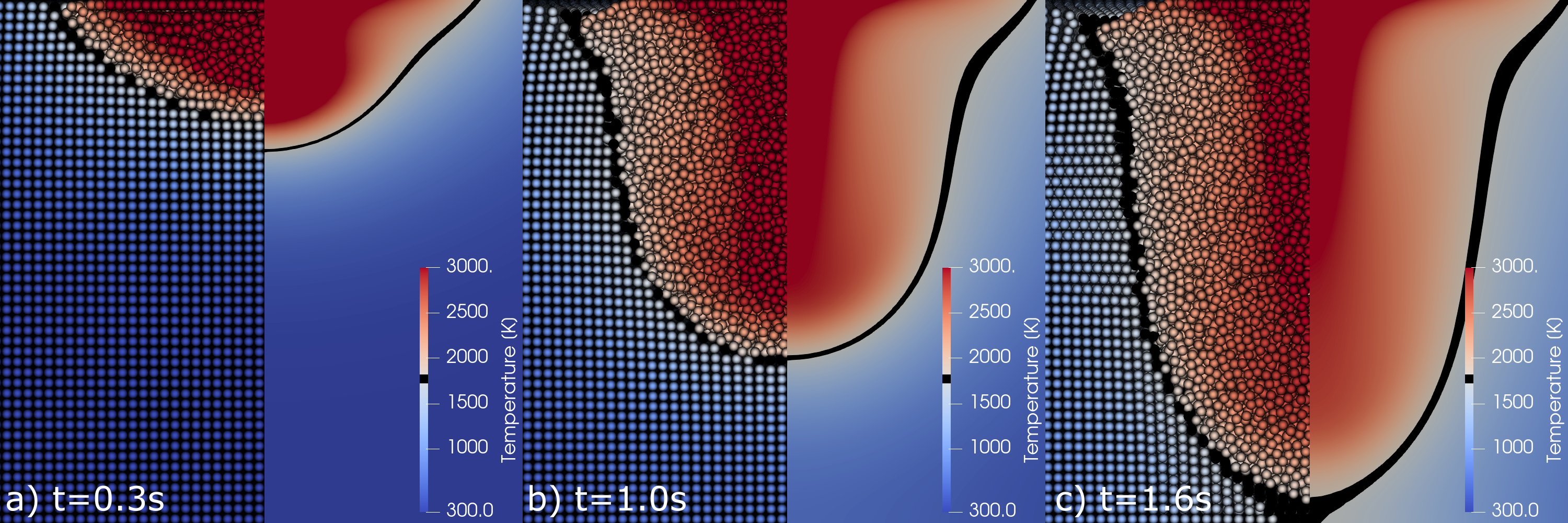
In many manufacturing processes of the SFB1120, effects at a free-moving surface play a decisive role and, at the same time, the melt does not represent a coherent area in many manufacturing processes. With the Eulerian methods used so far in the SFB, these moving surfaces can only be accurately represented by a significant increase in simulation complexity. At the same time, Lagrangian simulation methods, which allow a native and efficient treatment of these conditions, are receiving increasing attention in current research. In order to better understand the advantages of these methods, the Lagrangian method Smoothed Particle Hydrodynamics (SPH) has been investigated in a companion project for the simulation of gas metal arc welding (A04) as well as thermal spraying (A10), complementary to the previous numerical methods, since June 2021 as part of the 2nd phase of SFB1120. The investigations confirmed the high efficiency and flexibility of the method and led to a better understanding of the process flow field, heat transfer and solidification. Our findings and the benchmarks performed, as well as the increasing presence of this method in current research, lead to the conclusion that the method is very well suited for precise prediction of melting behavior.
Within the framework of this project, the unified SPH simulation of bodies of different phase states will first be developed and then investigated with respect to accuracy and robustness. In the next step, the method will be extended to simulate the heating, cooling and solidification process under consideration of volume contraction. Subsequently, the temperature-dependent component behavior (volume contraction and deformation) will be validated using experimental examples from the materials science subprojects A02 and A07, as well as the projects on aluminum casting (B08, B09). Finally, the improvement of the computational efficiency is investigated with the help of spatially adaptive methods, which allow to locally increase the spatial resolution in important areas of the simulation.
See also our papers:
Supported by the German Research Foundation (DFG)

In computer graphics the physically-based animation of rigid and deformable solids has many applications, ranging from special effects in games and movies to interactive training simulators. In some applications fracturing and cutting of solid objects plays an important role, e.g., in destruction scenarios in special effects production or medical simulators. Therefore, this project is dedicated to the development of new methods for the physically-based animation of cutting, tearing and fracturing.
In existing computer graphics approaches, the geometry of a solid is strongly coupled with the discretization that is required to numerically solve the equation of motion. Most often a tetrahedral or hexahedral mesh, which approximates the object domain, is used for discretization and cut or fracture surfaces are represented explicitly. Therefore, the discretization must be permanently adapted during a cutting or fracturing process. Most existing approaches are based on remeshing or voxelization. Remeshing based methods modify the discretization persistently to get a good approximation of the simulation objects and cut surfaces to produce accurate results. However, remeshing is computationally expensive, ill-shaped elements can lead to instabilities, and a parallelization of the corresponding code is non-trivial. Voxelization based approaches discretize the geometry using a regular hexahedral grid. In this way the elements stay well-shaped, the application of adaptive methods is simple, and code parallelization is feasible. However, the discretization must also be adapted permanently, the surface geometry can only be approximated, and many elements are required to represent a cut surface adequately.
In this project we will follow a different approach. The geometry of simulation objects and fracture surfaces should be completely decoupled from the discretization mesh. This will be realized by embedding an implicit representation of the solid's geometry into a regular hexahedral mesh using an extended finite element method (XFEM). This ensures well-shaped elements and simplifies the usage of adaptive methods and parallelization. In contrast to previous approaches, the discretization does not have to be adapted during a fracturing or cutting process and the number of elements stays constant. However, accurate results can be achieved since the proposed method considers partially filled elements. In this project, we aim to develop the described decoupling approach and subsequently extend the method to support complex progressive fracturing with branches.
See also our papers:
Supported by the German Research Foundation (DFG)
The goal of our project is the physically-based animation of elastic and elasto-plastic bodies with applications in computer graphics, e.g., virtual reality applications, digital games, and special effects. In many of these applications large deformations and complex collisions are crucial for practical applications, such as medical training simulators. Almost exclusively, Lagrangian simulation approaches are used in such settings today. Here, the bodies are represented as collections of mass points, which move with the body and which contain the degrees of freedom, in combination with a set of connectivity information (the mesh). Large deformations (e.g., resulting from strong collisions) cause problems as they lead to strong deformations of the simulation mesh. Single elements can quickly become degenerate or even inverted. As a consequence, the material models that are typically used become invalid. Approaches to circumvent these problems usually require complex and expensive re-meshing operations, and smaller time-steps, which lead to drastic increases in computation time. Nonetheless, these techniques cannot guarantee an inversion-free state. Other approaches resolve degenerate or inverted elements with unphysical modifications of the material model. This effectively reduces the accuracy of the simulation. Additionally, these approaches lead to discontinuities which, e.g., prevent the use of higher-order time integration schemes.
To solve the aforementioned problems we plan to develop simulation approaches based on Eulerian representations, which use a spatially fixed simulation grid for discretization. Such approaches have been prominent in the area of fluid simulation, while first attempts to use them for simulations of deformable bodies were only made very recently. These attempts indicate the potential of Eulerian methods, but the lack of research in the area leaves many problems unsolved. With our project we will address the most important problems. We will develop efficient and accurate simulators based on higher-order integrators, adaptive discretizations and methods for continuous collision detection and resolution. In addition, we will develop hybrid methods to combine advantages of Lagrangian and Eulerian representations, and investigate the simulation of progressive cuts and fracture. Finally, we want to develop algorithms for efficiently visualizing the results with the help of procedural synthesis to achieve highly detailed animations.
See also our papers:
Supported by the German Research Foundation (DFG)

The research topic of this project is the robust physically-based animation of deformable bodies in computer graphics. Physically-based animation has many application areas in computer graphics, e.g. virtual reality, computer games and special effects in movies and commercials.
In this project we focus on the animation of deformable volumetric bodies using continuum mechanical approaches. These approaches are widely-used in computer graphics since they allow a high degree of realism. The simulation is usually performed using finite element methods. For these methods a volumetric body must be discretized, e.g. using tetrahedral or hexahedral meshes. However, these meshes cause problems when simulating large deformations, which are essential in many computer graphics applications. Large deformations can occur locally, e.g. when two bodies collide. Such a deformation can lead to degenerate or inverted elements in the discretization mesh. These elements can cause unrealistic material behavior, numerical problems and even an abort of the simulation since different constitutive laws are not defined for inverted elements. A mesh with degenerate and inverted elements represents an invalid state in the simulation since such deformations are not possible in the real world.
In the application areas of mechanics and engineering sciences degenerate and inverted elements must be avoided in order to guarantee accurate simulation results. This is achieved e.g. by a restart of the simulation with an adapted discretization. In computer graphics and especially in interactive applications the performance and robustness of the simulation is the main goal, while accuracy is often of secondary importance. Since degenerate and inverted elements cannot be prevented reliably in dynamic simulations and a restart is not possible in interactive applications, different methods have been developed in computer graphics to allow a stable simulation even if ill-shaped elements occur. These methods modify the constitutive laws which yields a local error. However, this error is tolerated since visual plausible results can be achieved. Existing methods use heuristic approaches to resolve ill-shaped elements. But this resolution is often inconsistent and therefore causes artifacts, numerical problems and discontinuous elastic forces.
The goal of this project is the development of a novel numerical method to resolve degenerate and inverted elements consistently. This method should solve the above mentioned problems. The resulting continuous elastic forces allow to apply implicit integration methods of higher order which were neglected in computer graphics so far.
See also our papers:

The physically-based simulation of deformable solids, like elastic rods, cloth models and volumetric deformable bodies, is an important research topic of our group. In this research area we investigate accurate continuum mechanical simulation methods to simulate complex physical effects like lateral contraction, anisotropy or elastoplasticity. At the same time we develop very efficient and robust geometrically-motivated approaches for interactive environments. Our group developed new strain limiting methods, volume conservation techniques, adaptive finite element methods and efficient approaches to handle anisotropic and elastoplastic material behavior. We also investigated efficient parallelization techniques and developed fast GPU-based simulation approaches.
See also our papers:
and our open-source framework:

Rigid body dynamics simulation is an integral and important part of many modern computer tools in a wide range of application areas such as computer games, animation software for digital production, including special effects in film and animation movies, robotics validation, virtual prototyping, and training simulators, just to mention a few. Our research focuses on interactive rigid body dynamics simulation, a subfield that has evolved rapidly over the past 10 years and moved the frontier of runtime simulation to applications in areas where, until recently, only off-line simulation was possible. As a consequence, this changes the computer tools humans use and has great economical impact on society as a whole.
See also our papers:
and our open-source framework:
